本記事・論文について

　本記事では以下の論文の概略を示しつつ、論文読解のための知識をまとめる。

論文: Konishi, Takuya, et al. "Identifying Key Observers to Find Popular Information in Advance." IJCAI. 2016.

※ IJCAI（International Joint Conference on Artificial Intelligence; 国際人工知能会議）: 人工知能学会分野でトップの学術会議

本記事・論文について
論文の内容
論文読解の参考となる知識
論文を読んだ感想

論文の内容

論文の概要

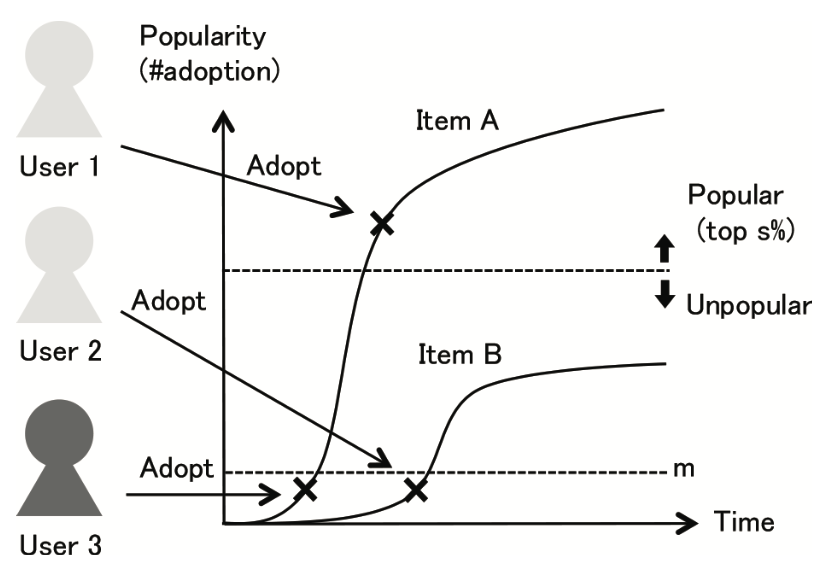
　本論文の目的は、観測者を経由して将来流行しそうなアイテムを前もって検出をすることである。 観測者（Observers）とは、流行する前から将来人気が出るアイテムを見つけられるユーザである。観測者をお気に入りリストに入れることで、ユーザは流行するアイテムを見つけることができる。

　アプローチは以下のようになる。

アイテムが流行するかどうかを判別する分類器を、他の人より先にアイテムを採用したユーザ集合を入力として設計する。
機械学習による特徴量選択を行うことで効率的な観測者を特定する。

流行するアイテムの早期検出の有効性

　消費者の購買行動について分類を行なっているイノベータ理論*1 がある。その中で、流行には敏感で自ら情報収集し判断を行う購買行動をとる Early Adaptors は、オピニオンリーダーとして他の消費者層に大きな影響を及ぼすとされる。

　流行するアイテムの早期検出に対して、以下のような利点の例がある。

企業のマーケティング戦略を効果的にできる*2。
他の研究チームより先に将来流行する研究分野を特定できる。
おいしいレストランを有名になる前に知ることができる。

　理論的には Early Adopters の存在は証明されているが、対象となる分野によって異なり、特定することは困難とされる。

観測者を経由した流行アイテムの早期検知

　本論文では、流行アイテムのEarly Adoptersを観測者（Observers）としている。観測者を経由することで、

ユーザ推薦への応用に対して簡単にカスタマイズすることが可能
エキスパートの行動から知識を獲得できる

f:id:farma_11:20171229015455p:plain — 観測者の選択の例（本論文から引用）

　一方で、以下のような課題がある。

膨大なユーザの中から観測者として適切なユーザを選び出すことは困難
既存研究 *3では、ユーザ間のネットワークが仮定されているため、電子商取引などのサービスに適用できない

　本論文では、機械学習を用いた特徴量選択を行うことで効率的に観測者を特定することを試みている。ユーザが選んだアイテムとタイムスタンプといったイベントデータのみの利用で、観測者の予測が可能になる。

　具体的な提案手法や評価実験等は、本論文や解説スライド（日本語）を参考にしてください。

論文読解の参考となる知識

（標準）シグモイド関数を用いた線形分類

　（標準）シグモイド関数（Sigmoid function）はロジステック回帰に用いられたり、NN（Neural Network）における活性化関数といてよく用いられる。

$\sigma(x) = \frac{1}{1 + \exp(-x)} = \frac{1}{2} \bigl( \tanh\bigl(\frac{x}{2} \bigr) + 1 \bigr)$

　シグモイド関数は以下のような性質を持つ。

$\lim_{x \to -\infty} \sigma(x) = 0, \lim_{x \to \infty} \sigma(x) = 1$ となり、値を確率としてみることも多い。
$\sigma(0) = 0.5$ であり、点 $(0, 0.5)$ に対して点対称となる。
微分可能である。（ $\sigma'(x) = (1 - \sigma(x)) \sigma(x)$ ）

　シグモイド関数を用いた2値分類をする際は、基本的には以下のようになる。

$y = \begin{cases} 1, (\sigma(x) \geq 0.5 \Leftrightarrow x \geq 0) \\ 0, (\sigma(x) < 0.5 \Leftrightarrow x < 0) \end{cases}$

f:id:farma_11:20171228005931p:plain — シグモイド関数を用いた2値分類

　以下は、シグモイド関数の描画のためのPythonのソースコードである。

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1) # -5.0から5.0まで0.1刻みで生成
y = sigmoid(x)

plt.plot(x, y) 
plt.show()

ワイブル分布（Weibull Distribution）*4

　信頼性データのモデル化に最も一般的に使用される連続確率分布である。製品の寿命予測などに用いられることが多い。

$p(z | k, \theta) = \begin{cases} \bigl( \frac{k}{\theta} \bigr) \bigl( \frac{z}{\theta} \bigr)^{k-1} \exp \biggl( - \bigl( \frac{k}{\theta} \bigr)^k \biggr), (z \geq 0) \\ 0, (z < 0) \end{cases}$

　パラメータ $k$ に対して、 $k = 1$ のとき指数分布、 $k = 2$ のときレイリー分布となる。

f:id:farma_11:20171229030955p:plain — ワイブル分布 $W(\theta, k)$ の形状

　以下は、ワイブル分布 $W(\theta, k)$ の描画のためのPythonのソースコードである。

import numpy as np
import matplotlib.pylab as plt

def weibullDistribution(z, th, k):
    return np.where(
        z < 0, 0, # z < 0 のとき0をとる
        (k/th) * ((z/th)**(k-1)) * np.exp(-(z/th)**k)
        )

x = np.arange(0.0, 6.0, 0.1) # 0.0から6.0まで0.1刻みで生成
y11 = weibullDistribution(x, 1, 1)
y23 = weibullDistribution(x, 2, 3)

plt.plot(x, y11, label="W(1, 1)")
plt.plot(x, y23, label="W(2, 3)")
plt.legend()
plt.show()

その他の関数について

ヒンジ関数（Hinge function）

　SVM（Support Vector Machine）の誤差関数として知られる関数。境界面そのものは際どいため、マージンを持たせる。

$[z]_{+} = \begin{cases} 0, (z \geq 1) \\ 1 - z, (otherwise) \end{cases}$

符号関数（Sign function）

　実数の符号に対して、-1、0、または1のいずれかを返す関数。

$sign(x) = \begin{cases} 1, (x > 0) \\ 0, (x = 0) \\ -1, (x < 0) \end{cases}$

論文を読んだ感想

　観測者を経由した流行アイテムの予測は、実際のサービスに対しても適用が十分可能なものであると感じた。また、本記事に取り上げている論文の内容はイノベータ理論にも関連があると感じ、記事に追加している。

*1:Rogers, Everett M. Diffusion of innovations. Simon and Schuster, 2010.

*2:Yu, Sheng, and Subhash Kak. "A survey of prediction using social media." arXiv preprint arXiv:1203.1647 (2012).

*3:Trusov, Michael, Anand V. Bodapati, and Randolph E. Bucklin. "Determining influential users in internet social networks." Journal of Marketing Research 47.4 (2010): 643-658.

*4:Weibull, Waloddi. "Wide applicability." Journal of applied mechanics 103.730 (1951): 293-297.

Farma's Study Desk

IJCAI2016: "Identifying Key Observers to Find Popular Information in Advance"